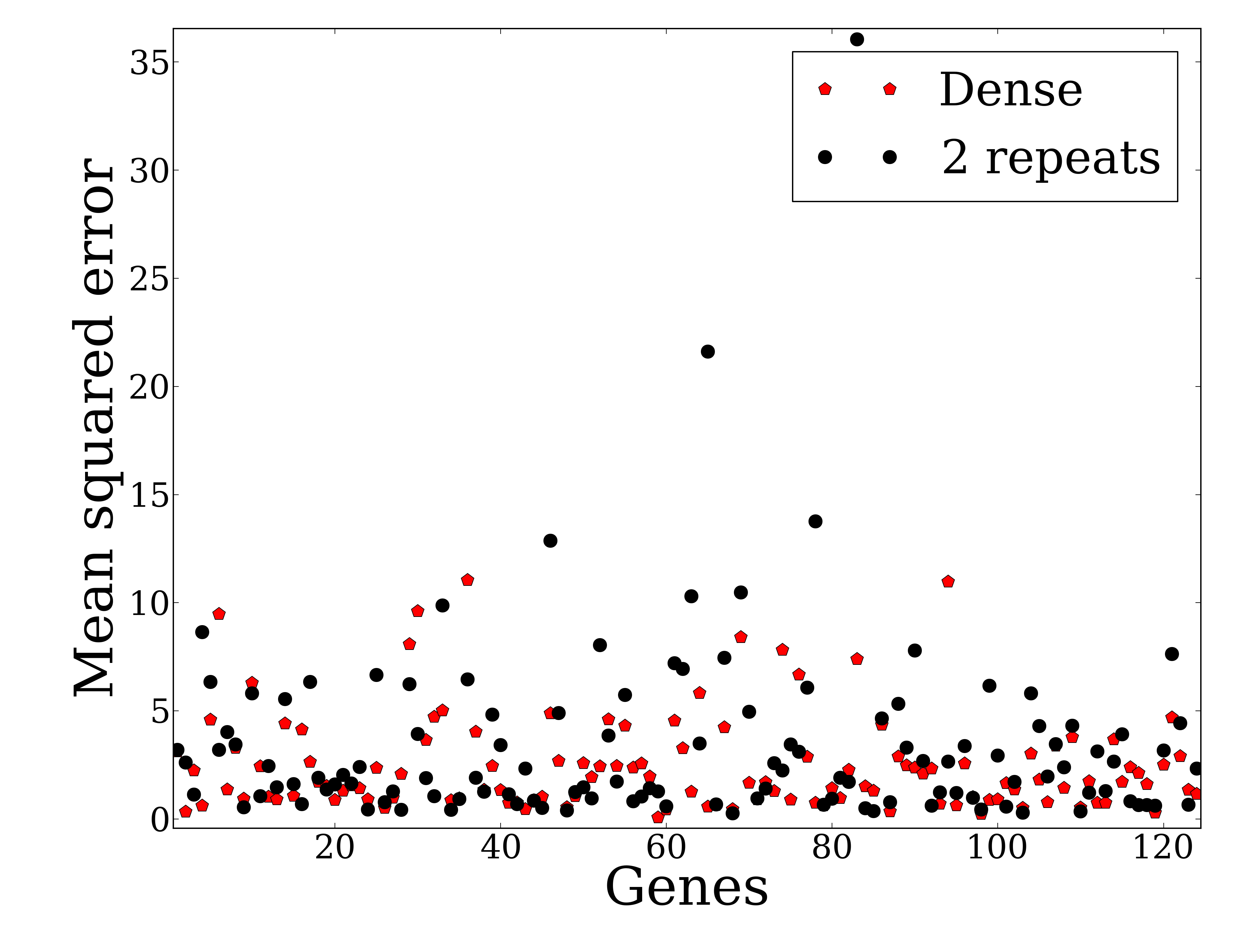
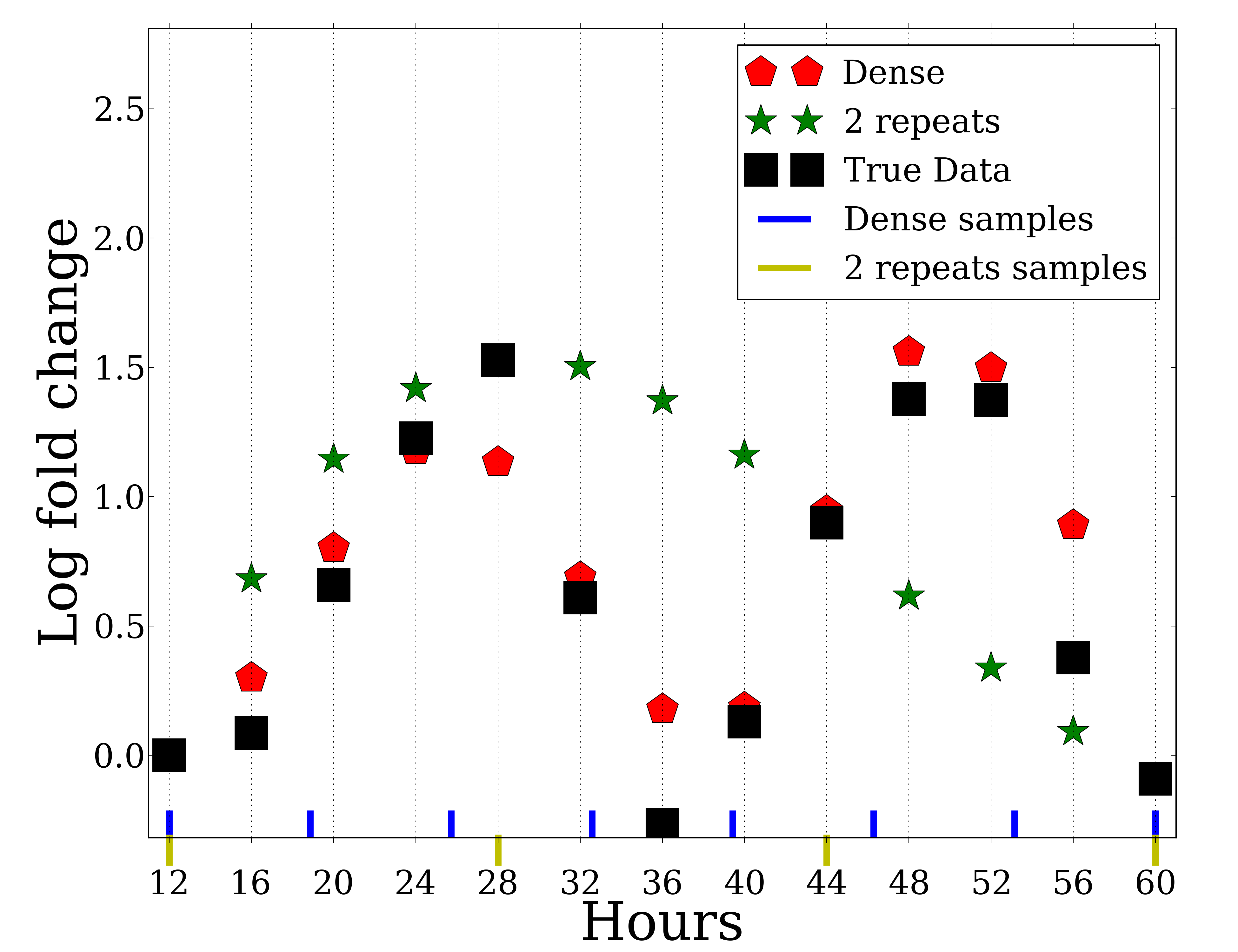
Recent advances in sequencing technologies have enabled high throughout profiling of several types of molecular datasets including mRNAs, miRNAs, methylation, and more. Many studies profile one or more of these types of data in a time course. An important experimental design question in such experiments is the number of repeats that is required for accurate reconstruction of the signal being studied. While several studies examined this issue for {\em static} experiments which are often assumed to profile independent samples (for example different patients) much less work has focused on the importance of repeats for time series analysis. Due to budget and sample availability constraints, more repeats in such studies often imply less time points and vice versa. Here we study this issue by comparing the performance of dense and repeat sampling of time series expression data. We first develop a theoretical framework that can analyze the expected error for these two strategies for a restricted yet expressive set of possible curves over a wide range of possible noise levels. We also analyze real expression data to compare these strategies. For both the theoretical analysis and experimental data we observe that under reasonable assumptions on noise, dense sampling usually outperforms the repeat strategy. Our results provide support to the large number of high throughput experiments that do not perform repeat measurements in each of the time points.